TRAIETTORIE
La Balistica esterna analizza tutti i fenomeni inerenti il moto del proiettile dal vivo di volata dell’arma fino al suo impatto sul bersaglio.
Nelle prime armi da fuoco si faceva uso di proiettili sferici in canne lisce. Uno dei primi studiosi di fisica che si dedicò all’analisi del moto del proiettile nell’aria introducendo i criteri della gravità e della parabola fu Galileo Galilei. Successivamente Newton abbinò, in modo sostanziale, i concetti di fisica e di algebrica alla balistica esterna ed introdusse il concetto della resistenza dell’aria.
Nel prosieguo degli anni, con l’utilizzo di proiettili oblunghi esplosi in canne con anima rigata che conferivano il moto rotatorio al proiettile, furono intrapresi studi di fisica e di matematica in uno con sperimentazioni pratiche che cercarono di rendere analitiche le formulazioni legate ai due movimenti del proiettile in contemporanea, ovvero la traslazione, l’avanzamento e la rotazione sul proprio asse.
Se un proiettile fosse esploso nel vuoto, sotto la spinta della carica di lancio lo stesso sarebbe animato da una determinata velocità iniziale che, in assenza di ogni altro fenomeno, farebbe sì che lo stesso proiettile conserverebbe all’infinito una traiettoria rettilinea e uniforme.
Ulteriori studi focalizzati sulle problematiche legate sia alla analisi che alla fisica cioè quelli riguardanti il moto del proiettile sotto le azioni esercitate dalle forze resistenti che quelli inerenti il moto assiale portarono alla introduzione di tavole balistiche.
Un proiettile che si muove nell’aria sarà condizionato dal suo peso, dalla sua velocità, dalla resistenza dell’aria e dalla forza di gravità.
Quando un proiettile viene esploso da una canna rigata esso percorrerà una distanza compresa tra la bocca dell’arma e il bersaglio nel lasso di tempo imposto dalla sua velocità.
Il percorso del proiettile non sarà assimilabile ad una linea retta ma sarà caratterizzato da una parabola discendente e, tale percorso viene chiamato “traiettoria”.
Pertanto:
Traiettoria: è la parabola percorsa dal proiettile
Origine della traiettoria: è il vivo di volata della canna dell’arma al suo centro
Orizzonte dell’arma: è la linea retta orizzontale che passa per l’origine della traiettoria
Linea di sito: è la retta tra il centro della volata dell’arma e il punto di impatto
Linea di tiro: è la retta tra la volata dell’arma e l’infinito
Alzo o Angolo di elevazione: è l’angolo che la linea di tiro fa con la linea di sito
Angolo d’impatto: è l’angolo formato dalla tangente alla traiettoria nel punto d’impatto con la linea di sito

La precisione di un’arma da fuoco è strettamente legata a criteri costruttivi che unitamente alla corretta scelta del munizionamento consentono l’ottimale stabilizzazione del proiettile.
In buona sostanza per ottenere una corretta stabilizzazione del proiettile, è necessario che vi sia una “comunione” tra le caratteristiche del proiettile (peso-lunghezza-forma) con il passo di rigatura dell’arma oltre che con il rapporto velocità-peso del proiettile stesso.
Qualora si commetta un errore di valutazione dei parametri non solo avremo rosate più disperse ma addirittura, e specie sulle lunghe distanze, corriamo il rischi di non colpire il bersaglio.
Specialmente con il tiro con arma lunga rigata, la disponibilità del mercato per ogni calibro d’arma offre passi di rigatura anche molto differenti tra loro, senza contare che, nel settore della ricarica, esistono palle per singolo calibro aventi pesi diversi tra loro; è quindi naturale che la scelta ottimale in riferimento binomio arma-munizione rappresenti un aspetto essenziale.
Ricercare il proiettile ottimale che sia correttamente stabilizzato in un determinato passo di rigatura richiede informazioni facilmente nella bibliografia corrente e sulle riviste di armi ma esso può essere calcolato utilizzando alcune formule oppure consultando programmi presenti nel web.
Aspetti Generali
Come accennato, il proiettile segue una traiettoria curvilinea che è influenzata da due fattori: la forza di gravità e la resistenza dell’aria.
La forza di gravità materializza i suoi effetti sul proiettile non appena questi esce dalla volata dell’arma. La resistenza dell’aria rallenta in maniera progressiva il proiettile stesso favorendo la sua caduta in quanto al decremento velocitario subentra l’attrazione gravitazionale che aumenta in funzione della perdita velocitaria.
Sul proiettile in funzione della sua forma esistono due importanti punti: il centro della massa (G) e il centro di spinta (C). Il centro della massa (o baricentro) è il punto nel quale esercitano la sua azione la forza di gravità; il centro di spinta è il punto nel quale vengono invece applicate le forze aerodinamiche (portanza e resistenza dell’aria). Il tutto può essere schematizzato come segue:
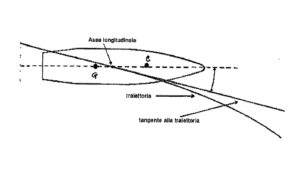
Poiché queste due forze agiscono in due punti diversi del proiettile, su di esso, si viene e creare una sorta di leva, che tende a ribaltare il proiettile nella sua traiettoria rettilinea ed è questo il motivo della ricerca della sua stabilizzazione.
La rigatura delle canne conferisce al proiettile il movimento giroscopico che, se gli equilibri in precedenza citati (peso-forma, carica di lancio e passo adottato) risultano corretti, la stabilizzazione giroscopica garantisce notevole precisione al bersaglio.
Se, i rapporti non sono corretti si possono innescare fenomeni perturbatori che inficiano la precisione.
Per meglio chiarire il fenomeno: riguardo alla stabilizzazione giroscopica del proiettile, possono essere presi come esempio i parametri del moto giroscopico della trottola o del fuso, dove, riferendoci a un proiettile, il piano dove essi girano è sostituito dalla resistenza dell’aria. Nel caso della trottola o del fuso noi sappiamo che se la velocità di rotazione è notevole essi pur ruotando velocemente restano fermi in un solo punto ma, al progressivo decremento della velocità di rotazione essi iniziano a prima a spostarsi poi a sbandare fino a ribaltarsi.
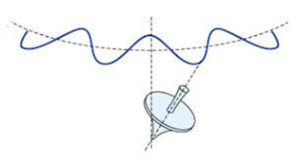
Il movimento giroscopico generato dalla rigatura della canna imprime al proiettile un movimento rotatorio intorno al suo asse longitudinale ma, a volte, diventa proprio tale movimento giroscopico la causa di instabilità a causa dei fenomeni così detti di precessione e nutazione.
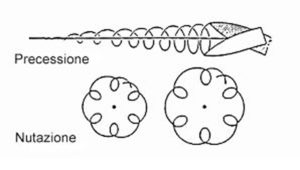
Dopo che un proiettile fuoriesce dalla volata della canna rigata, quindi caratterizzato dal movimento giroscopico molto elevato lungo il suo asse longitudinale, l’aria che agisce sul proiettile in volo genera una forza di disturbo che, a sua volta crea un momento ribaltante che tende a spostare l’asse del proiettile dalla sua posizione di riposo. A seguito di questo disturbo, l’apice del proiettile in volo presenta sempre, anche se in misure variabili, un movimento “oscillante” nel senso che la punta del proiettile è come se disegnasse nel suo percorso un piccolo cono intorno all’asse di rotazione con il proprio vertice sul suo baricentro e questo fenomeno è detto “precessione”.
Ma quando un proiettile con movimento giroscopico in volo subisce una perturbazione che tende a farlo ribaltare, al movimento di precessione si sovrappone un altro fenomeno, la “nutazione”. La nutazione fa si che l’asse del proiettile compia delle rotazioni sovrapposte a quella di precessione
Ma quest’ultimo movimento perturbatorio può anche dipendere da svariate cause: forma non corretta, imperfezioni di fabbricazione (ad esempio differenze di spessore del mantello), rinculo e imperfezioni della volata dell’arma etc. Tale movimento perturbatorio che, nella norma, ha inizio dalla punta del proiettile, qualora subentrano concause diverse dalla semplice precessione può tradursi anche in uno sbandamento e/o in un ribaltamento.
Quando un proiettile della giusta forma e peso in rapporto al passo di rigatura ed alla carica di lancio possiede la giusta velocità e segue la sua traiettoria, i movimenti perturbatori vengono progressivamente neutralizzati per azione dell’aria che opera una pressione uniforme sulla superficie del proiettile.
In tale condizione il proiettile può definirsi stabilizzato ma se un’’oscillazione non è di base neutralizzata, il proiettile già in partenza non è dinamicamente stabilizzato, e la sua perdita di precisione può anche tradursi in un ribaltamento.
Fino a quando un proiettile vola a velocità supersonica, il punto di interazione delle forze in gioco si trova in un punto intermedio tra la punta e il suo centro di gravità. Quando lo stesso dopo aver percorso una certa distanza inizia a perdere velocità, egli raggiungere la cosiddetta “fase transonica” cioè una velocità compresa tra 1,2 e 0,8 Mach. Quando un proiettile viene a trovarsi nella fase transonica, l’aerodinamica cambia in modo sostanziale. Il cambiamento si traduce in uno spostamento del suo centro di pressione che può indurre una instabilità dinamica spesso responsabile anche del completo ribaltamento.
Affinchè un proiettile possa evitare di passare nella fase transonica sarebbe meglio evitare di ingaggiare bersagli a distanze superiori alla portata della munizione e alla portata reale dell’arma che si utilizza.
COEFFICIENTE BALISTICO
All’ inizio del 1900 furono intrapresi studi, aventi un certo criterio, mirati ad individuare la giusta scelta di un proiettile in funzione di una data munizione e all’arma per questa impiegata.
Lo studio dell’aerodinamica di un proiettile, ovvero il suo comportamento nel compimento della traiettoria alle medie e lunghe distanze, raggiunse un concreto risultato con la stesura delle tavole del Lowry poi, successivamente semplificate da Ingalls; queste ultime erano in grado di giungere a un dato coefficiente a seconda della forma del proiettile e fu da tali tavole che si giunse alla individuazione dei “coefficienti balistici”.
In parole semplici, il “coefficiente balistico” altro non è che un indice di efficienza relativo alla forma del proiettile, cioè la misura della attitudine di un certo proiettile nel superare la resistenza dell’aria rispetto ad altri che diversamente risentono degli effetti perturbatori nella loro traiettoria.
In generale, la necessità di individuare un adeguato B.C. (Coefficiente Balistico) nasce per i tiri a lunga distanza.
Le palle da tiro specie quelle prodotte da fabbriche rinomate (es: Sierra, Hornady, Barnes etc) sono caratterizzate da un alto coefficiente balistico e finalizzate a raggiungere il bersaglio con traiettoria tesa ma esse, all’impatto si frammenteranno e quindi saranno poco adatte ad un utilizzo venatorio in quanto caratterizzate da minore potere d’arresto con conseguente minore cessione di energia cinetica.
Diversamente alcuni proiettili finalizzati all’attività venatoria, pur avendo un basso profilo aerodinamico (punta arrotondata e in piombo tenero) e quindi un basso B.C. si dimostreranno molto efficaci nell’abbattimento di selvaggina medio-grande.
Tirando le somme, il coefficiente balistico è un rapporto tra le prestazioni di un proiettile accuratizzato contro le prestazioni di un proiettile standard.
Quindi un confronto tra la resistenza all’aria che può avere un proiettile accuratizzato (ovvero la perdita di velocità subita per la resistenza dell’aria in volo) con la resistenza di un proiettile standard espresso dalla formula:

DENSITA’ SEZIONALE
Nell’ambito delle munizioni commerciali e in special modo in quelle particolarmente costose nell’interno della scatola esse hanno una tabella balistica e/o una scheda contenente i dati relativi al comportamento aerodinamico dei proiettili alle diverse distanze. Ovviamente questi dati, seppur riferiti a uno stesso calibro, saranno variabili in funzione del tipo di palla montato sulla cartuccia (a seconda che trattasi di palle Spire Point oppure Round Nose etc). In queste tabelle compare quasi sempre un dato molto importante per una completa conoscenza della balistica esterna, esso è: LA DENSITA’ SEZIONALE. Esso è il rapporto tra il peso e la sezione in cm2 di un proiettile.
La Densità Sezionale si calcola dividendo il peso del proiettile in grammi per la sezione del proiettile in cm. 2

